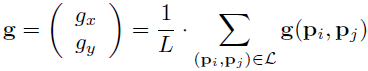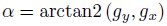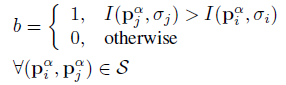原文:Stefan Leutenegger, Margarita Chli et al.《BRISK: Binary Robust Invariant Scalable Keypoints》
BRISK
摘要:从一幅图片中高效地寻找关键点始终是一个深入研究的话题,以此形成了众多的计算机视觉应用的基础。正在这个领域中。先驱算法SIFT和SURF在各种图形转换中表现出了巨大的性能。特别是SURF在日益更新的高性能方法中被觉得是计算最有效的方法。
本文提出的BRISK算法是用于关键点检測。描写叙述和匹配的一种新方法。在基准数据库中队BRISK的综合评价为:自适应和在大大降计算低成本下所表现的高质量的性能(这一些情况下。计算速度要比SURF快一个数量级)。速度的关键在于一种新的尺度空间的应用:基于FAST的检測器结合组装好的一位串描写叙述子,该描写叙述子从每一个关键点附近专门取样的强度比較检索得到的。
1.引言
将图像分解为本身感兴趣区域或特征区域是一种在计算机视觉中广泛应用的技术。用来减少当寻找原图像表面特征的复杂度。
图像表示﹑目标识别﹑匹配﹑三维场景重建以及运动跟踪都依赖于图像中稳定的具有代表性的特征。这个问题促进了研究并产生了大量的方法。
理想的特征点检測器发现突出的图像区域。这样以来虽然其角度变化。它们也能够反复检測特征点;更一般的是对于全部可能的图像转换它都得是稳健的。
相同地。理想的关键点检測器捕捉了最重要和独特的信息内容,这些内容包括在检測到的突出区域。这种话。假设遇到相同的结构区域也能够被识别出来。此外,在满足这些属性来实现所需的关键点的质量,检測器和描写叙述子的速度相同须要优化来满足手头任务的时间约束。
在原则上。最先进的算法目标在于即应用于严格要求的实验精度也应用于计算速度。Lowe’ 的SIFT 算法是一个眼下被广泛接受的最高质量的选择,对各种常见的图像转换具有有效的特殊性和不变性,然而,这种算法以计算代价为成本。在还有一方面,FAST关键点检測器和BRIEF方法的结合对描写叙述子提供了更实时应用的选择。然而虽然速度拥有明显的优势。但就可靠性和稳健性而言后一种方法更易接受,由于它具有最小的图像扭曲和旋转的承受度,尤其在平面旋转和尺度变换上更明显。
结果。像SLAM这种试试应用程序须要对数据关联运用概率性的方法来找到匹配一致性。
从图像中提取合适的特征点的内在困难在于平衡两个相互矛盾的目标:高质量的描写叙述子和低计算需求。这就是这项工作的目的。即用BRISK方法建立一个新的里程碑。
或许最相关的任务是解决问题:SURF已经演示了稳健性和速度的实现,仅仅是。要得到的结果非常明显。在花费更少的计算时间BRISK获得了更可观的匹配效果。简而言之,本文对从图像中得到特征点提出了一个新的方法,得到的要点例如以下:尺度空间特征点检測:图像和尺度维度都是通过使用一个显著性的标准来识别感兴趣特征点。为了提高计算效率。在图像金字塔的octave层和层于层的中间检測特征点。通过在连续域拟合二次函数来获得每个关键点的位置和尺度。关键点检測:由点组成的样本模式位于比例合适的同心圆上,在每个关键点的相邻位置使用该圆来检測灰度值:就地处理强度梯度。决定了特征描写叙述方向。最后。面向BRISK 的採样模式用于获得成对的亮度对照结果。将结果组合成二进制BRISK描写叙述子。
BRISK关键点一旦生成因为描写叙述子的二进制本质特点就能够很高效的匹配。强烈注意一下其计算速度,BRISK还利用存储SSE指令在今天的架构中提供了广泛的支持。
2.相关工作
在文献中质量近期最好的特征点提取方法是SIFT。高描写叙述力和鲁棒性来启示和观点改变使得评价SIFT描写叙述子在调查中处于最高位置。然而。这样的描写叙述子使得SIFT的高维度提取速度很慢。PCA-SIFT 使得描写叙述子从128维降到了36维。可是。影响其特殊性和添加描写叙述子形成的时间差点儿使得添加匹配速度的性能毁于一旦。这里值得注意的是,GLOH描写叙述符也属于类SIFT方法家族。也已经证明其具有独特性可是比SIFT要付出很多其它昂贵的计算。
对特征提出日益增长的高质量和快速度的需求已使得很多其它的算法研究可以以更高的速率处理大量的数据。
值得注意的是,Agrawal等人用中心对称的局部二值化模式作为还有一个SIFT方向直方图的方法。近期的BRIEF算法是超快速描写叙述符,匹配以及二进制串的组合设计的。包括了简单的图像增强在随机预定的像素位置的比較。
虽然这样的方法简单而且有效,但其对图像旋转和尺度变换很敏感。以此限制了其通用功能的应用。
可能眼下最吸引人的特征点提取方法是SURF,它已被证实比FAST 速度明显快非常多。SURF特征点检測使用了Hessian矩阵(blob检測器)的行列式,而其描写叙述符是总结了Harris小波在感兴趣区域的响应。SURF展示了令人深刻的最先进的计时,在速度方面,数量级仍然是远远不够最快的。眼下这些限制了其提取特征点的质量。
本文提出了一种新颖的算法称为BRISK,其具有高性能。高速的特征点检測和描写叙述符以及高速匹配。意如其名,该方法在非常大程度上具有旋转不变性和尺度不变性。实现了高性能和最先进的同一时候极大地减少了计算成本。以下的特征描写叙述子的方法是,眼下在基准数据库运行的实验结果和使用标准化的评价方法。即提出了关于SURF和FAST的BRISK评价。这被广泛地接受为在常见的图像转换领域内的比較准则。
3.BRISK
3.1 尺度空间的检測
注重计算效率,特征检測方法是Mair等人对图像感兴趣区域检測时的工作启示。他们的AGAST本质上是如今流行的FATS算法性能的扩展,被证明是特征提取的一个给出有效的基础。实现尺度不变性的目标对高质量的关键点是至关重要的,为了进一步得到极大值。不仅要在图像平面上研究。并且在尺度空间使用FAST分数作为精确地測量。虽然在粗轴上离散化尺度轴比选择高性能检測器更难,但BRIEF检測器预计了在每个连续的尺度空间的每个特征点的真实值。
在BRIEF的框架中。尺度空间金字塔的组成是n个octave层(用ci表示)和n个intra-octave层(用di表示),文章中n=4,i={0,1,...,n-1}。
如果有图像img,octave层的产生:c0层就是img原图像。c1层是c0层的2倍下採样,c2层是c1层的2倍下採样。以此类推。
intra-octave层的产生:d0层是img的1.5倍下採样。d2层是d1层的2倍下採样(即img的2*1.5倍下採样),d3层是d2层的2倍下採样,以此类推。则ci、di层与原图像的尺度关系用t表示为:,
这里重要的是要注意FAST和AGAST都为特征点检測的掩膜形状提供了不同的选择。在BRISK中,主要使用了9-16个掩膜,即在16像素的圆中至少须要9个连续的像素来提供足够亮或暗的像素来实现,相比于FATS标准的中心像素的实现。
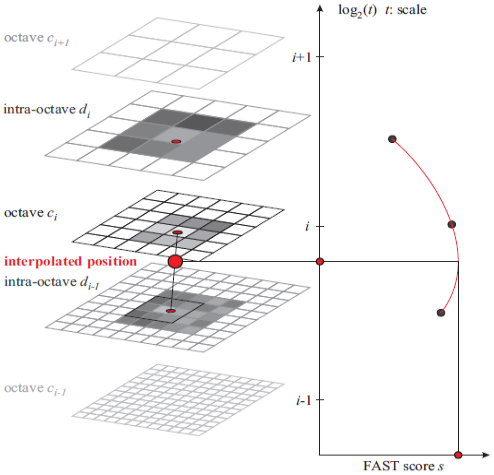

開始时,FAST 9-16 检測器在每个octave层和octave层分别使用相同的阈值T来识别潜在的感兴趣区域。接着。属于这些感兴趣区域的点在尺度空间上进行非极大值抑制(同SIFT算法 的非极大值抑制):首先,问题是特征点须要在每一层的FAST得分值s的8邻域内实现最大值条件。分值S定义为在一幅图像的块区域的点的最大阈值。其次。每一层及其上下层的得分值也要尽可能的低。检查相同大小的正方形邻域:在每一层中内部边长为2个像素的最可能是最大值。由于相邻层(因此其FAST的得分)代表有不同的离散化。对其邻域边界进行一些插值。
图1描写叙述了这个过程採样和极大值检測的一个样例。
尺度轴在octave c0层的最大值检測是一个特例:为了获得FAST分数,由于c0层是最底层,故需虚拟有一个d-1层,在c0上使用FAST5-8。
然而,在这样的情况下,d-1层patch的分数须要比检測的octave c0的特征点低。
考虑到图像的特点作为一个连续数字化不仅在图像上也在尺度维度上,为每个检測到的最大值运行亚像素插值和持续的进行。为了限制细化过程的复杂性,首先。满足一个二维最小二乘意义上的二次函数使得每3个score-patches(获得该层和上下两层的关键点)得到3像素突出最大值。
为了比較反复採样,考虑在每一层採用3x3的得分patch。接下来,这些突出的score用合适的一维曲线沿着尺度轴生成最后的得分预计和其最大值的尺度预计。最后一步,反复对图像坐标在该层及邻边决定性尺度进行插值。
BRISK检測在Boat序列的两幅图中是近距离的的一个样例如图2所看到的。
3.2 特征点描写叙述
给定一组特征点(包括亚像素插值图像位置和相关浮点型点的尺度值)。BRISK描写叙述子是由二进制串通过间接简单的亮度比較測试的结果组成。
这样的观点已证实是很有效的,然而在这里使用很多其它的定性模式。在BRISK中,确定了每一个特征点的特征方向以便得到方向均衡化的描写叙述子。因此,实现旋转不变性是一般鲁棒性的关键。同一时候,精心选择了注重描写叙述最大化的亮度比較。
3.2.1 採样模式和旋转预计
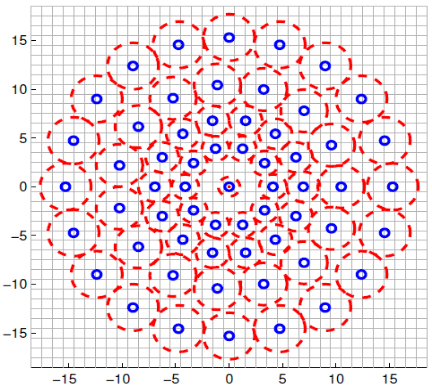
BRISK描写叙述子关键的概念是利用採集关键点相邻位置所使用的模式。该模式如图3所看到的,以关键点为中心,在其周围採集N个特征点的圆。定义多个相等局部圆形区域。这样的模式类似于DAISY描写叙述符,重要的是要注意到在BRISK中所使用的是全然不同的,DAISY专门为密集匹配建立的,刻意地捕捉很多其它的信息,因此,要求速度和存储需求。
为了避免混叠效果。对在模式中的採样点Pi应用了高斯平滑。标准差δi正比于每一个採样点相应于各自中心的距离,定位和扩展模式在图像中相应地为关键点k模式化,考虑一个N(N-1)/2个採样点对。用集合(Pi。Pj)表示。
这些点的平滑像素值分别为I (Pi , σi ) 和I (Pj , σj ),用于预计局部梯度值g(Pi , Pj ) 的公式为:
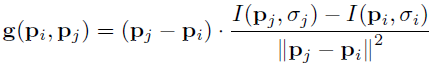
全部组合方式的集合称作採样点对,用集合表示为:
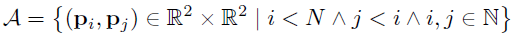
定义短距离点对子集S、长距离点对子集L(L个)为:
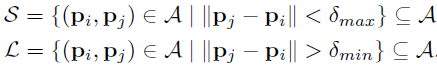
当中,阈值距离设置为:δmax=9.57t。δmin=13.67t。t是特征点k所在的尺度。
如今要利用上面得到的信息,来计算特征点k的主方向(注意:此处仅仅用到了长距离点对子集)。例如以下:
长距离的点对都參与了运算,基于本地梯度互相抵消的假说,所以全局梯度的计算是不必要的。这一点同一时候也被距离变量阈值δmin 的实验确认了。
3.2.2 创建描写叙述子
对于旋转和尺度归一化的描写叙述子的建立,BRISK使用了关键点k周围的抽样点旋转α = ARCTAN2 (gy , gx )角度作为模式。和BRIEF类似。BIRSK的描写叙述子也是一个包括512个比特位的向量,每一个描写叙述子由短距离点对(Pαi , Pαj ) ∈ S两两进行比較产生的,上标alpha表示旋转的模式。这种每一位b相应于:
与BRIEF不同的地方是,BRIEF仅仅是进行亮度比較,除了预设尺度和预先对样本模式的旋转之外,BRISK和BRIEF有着根本的差别:一.BRISK使用固定的样本模式点。并且是以R为半径环绕关键点周围的圆进行均匀取样。
因此特定的高斯核平滑不会突然地扭曲亮度内容的信息(模糊邻近的两个採样点的亮度,从而保证亮度平滑过渡)二.与两两组成的点对照BRISK显著的降低了採样点的数量(比如,单个的样本点參与了很多其它的比較),限制了亮度查找表的复杂度三.这里的比較是受到空间的限制的,所以亮度的改变仅仅仅仅是须要局部一致性就能够了。
对于上面的採样模式和距离阈值,获得了一个长度为512个比特位串。BIRSK64的描写叙述子也是一个包括512个比特位的向量,因此为一对描写叙述子匹配将以相同的速度进行定义。
3.3 描写叙述符匹配
匹配两个BRISK描写叙述符是简单的计算他们在BRIEF中汉明距离:比特位数量是不同的两个描写叙述符它们的衡量是不同的。注意他们各自通过位计数来降低按位操作的运算操作。在今天的架构中它们都能够很有效地计算。
3.4 实现说明
这里。对一些方法实现的问题给出了一个简短的概述,这些问题对总体的计算性能和该方法的重现性具有显著的贡献。全部基于OpenCV的常见的二维特征点界面的BRISK功能都能够用存在的特征点提取算法(SIFT,SURF, BRIEF, 等等)简单的整合和互换。
为计算显著性得分检測过程使用了AGAST算法实现。非最大值抑制受益于早期的终止能力,以此限制了显著得分计算到最小值。建立图像金字塔使用了一些SSE2和SSE3指令,这两个指令都是关于半抽样以及下抽样的1.5倍。
为了有效地用採样模式检索灰度值,生成了一个离散旋转的和已尺度化的BRISK模式版本号的查找表,包含取样点的位置和高斯平滑内核的属性以及长短距离配对的索引,这些消耗了大约40MB的RAM内存,全部这些仍然可接受受限的计算能力低的应用。另外,在一个简化的高斯内核版本号使用积分图像,使用的激励该内核为:在没有不论什么添加计算复杂度的情况下改变σ时内核是可伸缩变换的。在最后的实现中,在浮点边界和边长为ρ = 2.6 · σ使用了一个简单的平方均值滤波器误差预计。因此,不须要在整幅图片中使用很多不同内核的高斯平滑来浪费时间,而是使用一个随意的參数σ检索单个值。本文还整合改进了SSE汉明距离的測量来实现眼下OpenCV六倍的速度来实现匹配,比如带有BRIEF的OpenCV版本号。
4 实验
本文提出的方法在广泛地測试后,如今在首先由 Mikolajczyk 和 Schmid提出的领域中建立了评价方法和数据库。为了在其它的工作提出一致性的结果,本文也使用了在线的MATLAB评价版本号。每个数据库包括了一个六个图像的序列,变现出越来越多的转换数量。这里全部的比較都在每个数据库上对照第一张图片实现的。图4显示了一幅分析每个数据集的图片。

这个变换包括了角度改变(Graffiti 和 Wall),缩放和旋转(Boat),滤波(Bikes and Trees),亮度变化(Leuven)。以及JPEG压缩(Ubc)。由于角度变化场景是平面的,相比于OpenCV2.2版本号的SIFT和OpenCV初版的SURF。在全部序列的图像对上提供了一个地面真实的单一性矩阵用于BRISK的检測和描写叙述器的展示。
评估使用了相似性匹配,该匹配觉得每对特征点的描写叙述子距离都低于某个阈值匹配。比如相比于近期邻匹配。用最低的描写叙述子距离来寻找数据库的位置。
最后,展示了BRISK在属比較计时的计算速度方面的一大优势。
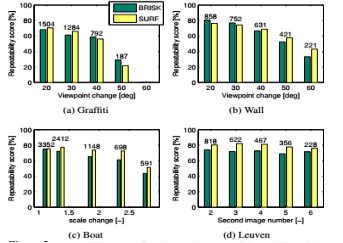
4.1 BRISK检測反复性
检測反复性定义为,在两幅图中计算对应的关键点和最小关键点的数量。
对应标志是通过查看一幅图中关键点区域的重叠区域(即提取圆)和从其它图形中得到的关键点区域的投影:假设相交的区域大于共同区域的50%,就被觉得是一个对应标志。用这样的方法标记在非常大程度上依赖于关键点圆形区域的工作,即尺度和半径之间的常数因子。
像这样选择用BRISK检測器获得的平均半径和SURF和SIFT获得的平均半径大致匹配。
反复性评价得分(选择的结果如图5所看到的)在一个序列中实施使用连续的BRISK检測阈值。为了达到与SURF检測器相当的比較,选择使用了各自的Hessian阈值在相似的主要的匹配步骤下使其大概输出一样的对应标志数量。
如图5所看到的,BRISK检測器展示了和SURF一样的反复性仅仅要应用的图像转换不是非常大。然而鉴于在计算速度上BRISK比SURF更具有明显的优势,本文提出的BRISK方法成为了强有力的竞争对手,即使在大尺度变换上似乎也稍逊一筹。
4.2 整体评价和比較BRISK算法
由于任务的目的在于提供一个整体及速度快有具有健壮性的检測器。描写叙述子和匹配,所以评估了BRISK中相比于SIFT和SURF的全部步骤的共同表现。图6 显示了在选择不同数据集的图像对,准确性-记忆曲线使用基于阈值的相似匹配。对这个评估又适应于检測阈值,以此输出一个在公平的意识下对应标志大致相等的数量。注意这里的评价结果与[3]中的不同,那里全部的描写叙述子都是在同样的区域中提取的(用Fast-Hessian获得的)。
如图6 所看到的。BRISK在全部数据集上比SIFT和SURF更有竞争优势。甚至在一些情况下远远胜过其它两个。
BRISK在树的数据集上的减少性能是因为检測器的性能:当SURF检測到2606和2624图像区域时,BRISK在图像4中仅仅检測到2004个图像区域,相比于在图片1中找到5949个图像区域,实现了对应标志的大致相等的数量。这个方案相同适用于其它的滤波数据集,Bikes:FAST的突出本质上比其它的类blob检測子更敏感。
因此,显示了从SURF区域中为树的数据集提取BRISK描写叙述子的评价。
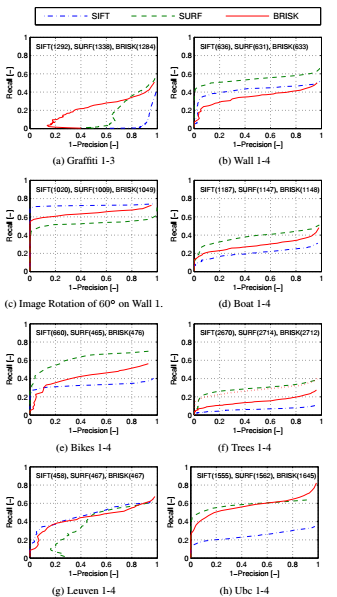 图6
图6 显然,SIFT在图Trees, Boat, 和Ubc datasets中的性能明显恶化。这能够解释在这些情况下检測器反复性受限的原因。还有一方面。SIFT和BRISK处理纯平面旋转的重要情况非常好,比SURF更好。
为了完毕实验的这个部分。联系到了BRIEF算法。图7 显示了不具有旋转的单尺度的BRISK版本号(SU-BRISK)和64字节的BRIEF特征点在同样的(单尺度)AGAST特征点上的比較。还包含了旋转不变性,单尺度的BRISK(S-BRISK)以及标准的BRISK。实验用两幅图像对进行:一方面使用了前两幅图片。在图Wall数据集中证明SU-BRISK和BRIEF64在没有单尺度和平面旋转的情况下都表现出非常相似的性能。注意到。BRIEF算法设计的真实条件。
还有一方面,应用不同的版本号到图Boat序列的前两幅图片:本次试验显示了一些就小规模旋转和尺度变化的鲁棒性而言SU-BRISK比BRIEF更让你更具有优势。此外。众所周知的和明显代价的旋转和尺度不变性是非常easy观察到的。
4.3 时间安排
时间控制已经记录在配备四核i7 2.67 GHz处理器(尽管仅仅用了一个核)执行Ubuntu 10.04 (32位)的笔记本电脑中,使用了上面具体的实现和设置过程。表1 给出了有关在图Graffit序列的第一幅图片的检測结果。而表2 显示了匹配时间。
执行平均值超过了100次。
注意到。全部的匹配器在没有不论什么提前终止优化的前提下都做了暴力描写叙述符距离计算。
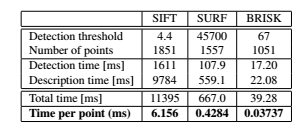
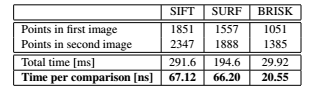
计时显示了BRISK的一个明显的优势,它的检測盒描写叙述子的计算通常比SURF的速度快一个数量级,这被觉得眼下存在的最快的具有旋转不变性和尺度不变性的特征点匹配。
相同重要的是。要强调BRISK能够easy更快地运行尺度化,通过在以匹配质量为代价的模式下降低採样点的数量。这是一个特定的应用下可能承担得起。
此外。尺度或旋转不变性能够省略,在不须要的应用上添加速度和匹配质量。
4.4 样例
对以上的提出补充广泛的评价,也提供了一个使用BRISK作为匹配的真实样例。图8显示了一幅图像对展现了各种变换。一个阈值为90的相似性匹配在没有明显的异常值得情况下得到的鲁棒性匹配(超过512对特征点)。
 图7
图7 5 结论
本文提出了一种新颖的方法称之为BRISK,攻克了经典的计算机视觉的检測问题,在现场和照相位置没有足够的先验知识下描写叙述和匹配图像关键点。
相比之下。与已建立且证明具有高性能的算法如SIFT和SURF相比。本文的方法实在地提供了一个戏剧性更快的按可比的匹配性能的选择,基于一个广泛评价的一份声明中使用既定的框架。
BRISK依赖一个简单地可配置的圆形的採样模式,模式从它形成一个二进制描写叙述符字符串计算亮度的对照。BRISK的独特特性可用于广泛的应用,特别是对硬实时约束或有限的计算能力。
最后,BRISK在费时的应用中提供了高端的特征点质量。
在对BRISK进一步研究的道路上,目标是探索能替代尺度空间最大值收索突出得分到生成更好高的可反复性,同一时候保持速度。此外,目标在于分析理论和实验上的BRISK模式和配置的比較,这种描写叙述子的信息内容或鲁棒性是最大化的。